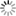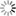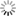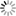Bendel 2-parameter function

This functional form is widely used to describe proton-induced SEU cross-sections. It is a modification of the Bendel 1-parameter fit, introduced by W.L. Bendel in 1983. It is a purely empirical functional form, and it has been shown to provide a better description of the cross-section data than the 1-parameter fit for many devices.

The Bendel-2 parameter function is described by two parameters, traditionally called "A" and "B". The functional form is somewhat complicated but may be written as follows:

F(E) = (B/A)¹⁴ [1.-exp(-0.18y^1/2 )]⁴

where

y(E) = (E-A) (18/A)^1/2 if E > A

= 0 otherwise.

For application to proton-induced SEUs, E is the proton energy in MeV and F(E) is the cross-section in units of 10^-12 cm²/bit.

For more information on the Bendel 2-parameter fit, see:

W.J. Stapor, J.P. Meyers, J.B. Langworthy, and E.L. Petersen, "Two Parameter Model Calculations for Predicting Proton Induced Upsets", IEEE Transactions on Nuclear Science, NS-37, 1966 (1990).

For more information on the Bendel 1-parameter fit, see:

W.L. Bendel and E.L. Petersen, "Proton Upsets in Orbit", IEEE Transactions on Nuclear Science, NS-30, 4481 (1983).

Both Bendel functional forms, as well as the Weibull function, are available for characterizing proton-induced SEU cross-sections in the CREME96 PUP routine.

Note: the Bendel 2-parameter fit described above is widely used. However, it is somewhat awkward in that the "B" parameter has no direct physical interpretation. An alternate formulation of the two-parameter model was given by:

Y. Shimano et al. , "The Measurement and Prediction of Proton Upsets ", IEEE Transactions on Nuclear Science, NS-36, 2344 (1989).

This alternate formulation uses two parameters, "S" and "A", which conveniently separate the asymptotic cross-section and energy dependence, respectively. In this formulation,

F(E) = S [1.-exp(-0.18y^1/2 )]⁴

where S is the asymptotic cross-section (in units of 10^-12 cm²/bit) and "y" is as given above.